2ND YEAR (B.TECH)
COMPUTER SCIENCE AND ENGINEERING
RTMNU , NAGPUR
SUB- SYATEM PROGRAMMING
Unit :- 5
Compiler:-
·
Compiler is a
translator program that translates a program written in (HLL) the source
program and translate it into an equivalent program in (MLL) the target
program.
·
As an important
part of a compiler is error showing to the programmer.
·
Executing a
program written n HLL programming language is basically of two parts. the
source program must first be compiled translated into a object program.
·
Then the results
object program is loaded into a memory executed.
Interpreter:-
·
An interpreter is
a program that appears to execute a source program as if it were machine
language.
· Languages such as
BASIC, SNOBOL, LISP can be translated using interpreters. JAVA also uses
interpreter. The process of interpretation can be carried out in following
phases.
1.
Lexical analysis
2.
Syntax analysis
3.
Semantic analysis
4. Direct Execution
TRANSLATOR
· Translator is a
program that takes as input a program written in one language and produces as
output a program in another language.
· The translator
performs another very important role, the error-detection. Any violation of d
HLL specification would be detected and reported to the programmers.
· Important role of
translator are:
1) Translating the HLL
program input into an equivalent ml program.
2) Providing diagnostic messages wherever the programmer violates specification of the HLL.
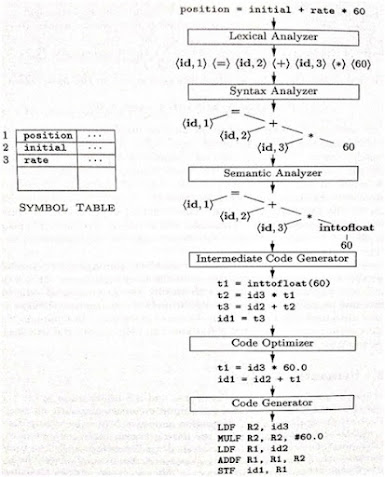
PHASES OF A
COMPILER:
A compiler
operates in phases. A phase is a logically interrelated operation that takes
source program in one representation and produces output in another
representation.
Lexical Analysis:-
·
The
first phase of scanner works as a text scanner. This phase scans the source
code as a stream of characters and converts it into meaningful lexemes.
·
Lexical analyzer represents these lexemes in
the form of tokens as:
·
Example
<token-name, attribute-value>
Syntax Analysis:-
·
The next phase is
called the syntax analysis or parsing. It takes the token produced
by lexical analysis as input and generates a parse tree (or syntax tree).
·
In this phase, token
arrangements are checked against the source code grammar, i.e. the parser
checks if the expression made by the tokens is syntactically correct.
Semantic Analysis:-
·
Semantic analysis
checks whether the parse tree constructed follows the rules of language.
·
For example,
assignment of values is between compatible data types, and adding string to an
integer. Also, the semantic analyzer keeps track of identifiers, their types
and expressions; whether identifiers are declared before use or not etc.
·
The semantic analyzer
produces an annotated syntax tree as an output.
Intermediate Code
Generation:-
·
After semantic
analysis the compiler generates an intermediate code of the source code for the
target machine.
·
It represents a
program for some abstract machine. It is in between the high-level language and
the machine language.
·
This intermediate code should be generated in
such a way that it makes it easier to be translated into the target machine
code.
Code Optimization:-
·
The next phase does
code optimization of the intermediate code. Optimization can be assumed as
something that removes unnecessary code lines, and arranges the sequence of
statements in order to speed up the program execution without wasting resources
(CPU, memory).
Code Generation:-
·
In this phase, the
code generator takes the optimized representation of the intermediate code and
maps it to the target machine language.
·
The code generator
translates the intermediate code into a sequence of (generally) re-locatable
machine code. Sequence of instructions of machine code performs the task as the
intermediate code would do.
Symbol Table:-
·
It is a data-structure
maintained throughout all the phases of a compiler. All the identifier's names
along with their types are stored here.
·
The symbol table makes
it easier for the compiler to quickly search the identifier record and retrieve
it. The symbol table is also used for scope management.
Example
LEXICAL ANALYSIS- ROLE OF FINITE STATE
AUTOMATA IN LEXICAL ANALYSIS
Lexical Analysis:-
·
Lexical
Analysis is the first
phase of compiler design where input is scanned to identify tokens.
·
A lexeme is an
instance of a token. A token is a sequence of characters representing a unit of
information in the source program.
Generating a lexical analyzer:-
·
A lex or flex is a program that is used
to generate a lexical analyzer. These translate regular definitions into C
source code for efficient lexical analysis.
Role of
Finite Automata:-
·
Specification of tokens by use of regular expressions.
·
Construction of a finite automata equivalent to a regular expression.
·
Recognition of tokens by a constructed finite automaton.
·
Correlation of error messages with the source code.
·
Removal of white spaces and comments from source program.
·
Expansion of macros if found in source program.
·
Identification of tokens.
·
Reading of input characters from source program.
FINITE AUTOMATON
· A recognizer
for a language is a program that takes a string x, and answers “yes” if x
is a sentence of that language, and “no” otherwise.
· The recognizer of the tokens as a finite automaton.
· A finite automaton can be: deterministic (DFA) or non-deterministic (NFA)
· This means that we may use a
deterministic or non-deterministic automaton as a lexical analyzer.
· Both deterministic and
non-deterministic finite automaton recognizes regular sets.
· Which one?
–
deterministic
– faster recognizer, but it may take more space
–
non-deterministic
– slower, but it may take less space
–
Deterministic
automatons are widely used lexical analyzers.
· First, we define regular expressions
for tokens; Then we convert them into a DFA to get a lexical analyzer for our tokens.
Non-Deterministic
Finite Automaton (NFA)
· A non-deterministic finite automaton
(NFA) is a mathematical model that consists of:
o
S
- a set of states
o
Σ
- a set of input symbols (alphabet)
o move - a transition function move to map state-symbol pairs to sets of states.
o s0 - a start (initial) state
o
F-
a set of accepting states (final states)
· ε- Transitions are allowed in NFAs.
In other words, we can move from one state
to another one without consuming any symbol.
· A NFA accepts a string x, if and only
if there is a path from the starting state to one of accepting states such that
edge labels along this path spell out x.
Example
Deterministic
Finite Automaton (DFA)
·
A Deterministic
Finite Automaton (DFA) is a special form of a
NFA.
·
No state has ε- transition
·
For each symbol a and state s, there
is at most one labeled
edge a leaving s. i.e. transition
function is from pair of state-symbol to state (not set of states)
Example:
Design of lexical analyzer:-
Converting RE to NFA
·
This is one way
to convert a regular expression into a NFA.
·
There can be
other ways (much efficient) for the conversion.
·
Thomson’s
Construction is simple and systematic method.
·
It guarantees
that the resulting NFA will have exactly one final state, and one start state.
·
Construction
starts from simplest parts (alphabet symbols).
· To create a NFA for a complex regular expression, NFAs of its sub-expressions are combined to create its NFA.
To recognize an empty string ε:·
To recognize a
symbol a in the alphabet Σ:
For regular expression r1 | r2:
N(r1) and N(r2) are NFAs for regular expressions r1 and r2.
·
For regular
expression r1 r2
Here, final state of N(r1) becomes the final state of N(r1r2).
·

For regular expression r*
· Example:
· For a RE (a|b) * a, the NFA construction is shown below.
Converting NFA to DFA (Subset Construction)
merge together NFA states by looking at them from the point of view of the input characters:
· From the point of view of the input, any
two states that are connected by an –transition may as well be the same, since
we can move from one to the other without consuming any character. Thus states
which are connected by an -transition will be represented by the same states in
the DFA.
· If it is possible to have multiple
transitions based on the same symbol, then we can regard
a transition on a symbol as moving from a state to a set of states (ie. the union of all those states reachable by a transition on the current symbol). Thus these states will be combined into a single DFA state.
To perform this operation, let us define two functions:
· The -closure function takes a state and returns the set of states
reachable from it based on (one or more) -transitions. Note that this will always
include the state itself. We should be able to get from a state to any state
in its -closure without consuming any input.
·
The function
move takes a state
and a character, and returns
the set of states reachable by one transition on this character.
·
Syntax Analysis – Context Free Grammar
Parser














0 Comments